In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations. To find a solution, the solver needs to use the provided equations to find the exact value of each variable. Generally, the solver uses either a graphical method, the matrix method, the substitution method, or the elimination method. Some textbooks refer to the elimination method as the addition method, since it involves adding equations (or constant multiples of the said equations) to one another, as detailed later in this article.
This is a set of linear equations, also known as a linear system of equations:
The solution of this system is:
This is a set of linear equations, also known as a linear system of equations:
The solution of this system is:
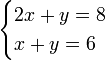

0 comments:
Post a Comment