In mathematics and science, a wave is a disturbance that travels through space and time, usually accompanied by the transfer of energy.
Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass transport. They consist instead of oscillations or vibrations around almost fixed locations. For example, a cork on rippling water will bob up and down, staying in about the same place while the wave itself moves onwards.
One type of wave is a mechanical wave, which propagates through a medium in which the substance of this medium is deformed. The deformation reverses itself owing to restoring forces resulting from its deformation. For example, sound waves propagate via air molecules bumping into their neighbors. This transfers some energy to these neighbors, which will cause a cascade of collisions between neighbouring molecules. When air molecules collide with their neighbors, they also bounce away from them (restoring force). This keeps the molecules from continuing to travel in the direction of the wave.
Another type of wave can travel through a vacuum, e.g. electromagnetic radiation (including visible light, ultraviolet radiation, infrared radiation, gamma rays, X-rays, and radio waves). This type of wave consists of periodic oscillations in electrical and magnetic fields.
A main distinction is between transverse waves, in which the disturbance occurs in a direction perpendicular (at right angles) to the motion of the wave, and longitudinal waves, in which the disturbance is in the same direction as the wave.
Waves are described by a wave equation which sets out how the disturbance proceeds over time. The mathematical form of this equation varies depending on the type of wave.
Contents[show] |
General features
A single, all-encompassing definition for the term wave is not straightforward. A vibration can be defined as a back-and-forth motion around a reference value. However, a vibration is not necessarily a wave. Defining the necessary and sufficient characteristics that qualify a phenomenon to be called a wave is flexible.The term wave is often understood intuitively as the transport of spatial disturbances that are generally not associated with motion of the medium occupying this space as a whole. In a wave, the energy of a vibration is moving away from the source in the form of a disturbance within the surrounding medium (Hall 1980, p. 8). However, this notion is problematic for a standing wave (for example, a wave on a string), where energy is moving in both directions equally, or for electromagnetic / light waves in a vacuum, where the concept of medium does not apply. There are water waves in the ocean; light waves from the sun; microwaves inside the microwave oven; radio waves transmitted to the radio; and sound waves from the radio, telephone, and person.
It may be seen that the description of waves is accompanied by a heavy reliance on physical origin when describing any specific instance of a wave process. For example, acoustics is distinguished from optics in that sound waves are related to a mechanical rather than an electromagnetic wave-like transfer / transformation of vibratory energy. Concepts such as mass, momentum, inertia, or elasticity, become therefore crucial in describing acoustic (as distinct from optic) wave processes. This difference in origin introduces certain wave characteristics particular to the properties of the medium involved (for example, in the case of air: vortices, radiation pressure, shock waves, etc., in the case of solids: Rayleigh waves, dispersion, etc., and so on).
Other properties, however, although they are usually described in an origin-specific manner, may be generalized to all waves. For such reasons, wave theory represents a particular branch of physics that is concerned with the properties of wave processes independently from their physical origin.[1] For example, based on the mechanical origin of acoustic waves there can be a moving disturbance in space–time if and only if the medium involved is neither infinitely stiff nor infinitely pliable. If all the parts making up a medium were rigidly bound, then they would all vibrate as one, with no delay in the transmission of the vibration and therefore no wave motion. On the other hand, if all the parts were independent, then there would not be any transmission of the vibration and again, no wave motion. Although the above statements are meaningless in the case of waves that do not require a medium, they reveal a characteristic that is relevant to all waves regardless of origin: within a wave, the phase of a vibration (that is, its position within the vibration cycle) is different for adjacent points in space because the vibration reaches these points at different times.
Similarly, wave processes revealed from the study of waves other than sound waves can be significant to the understanding of sound phenomena. A relevant example is Thomas Young's principle of interference (Young, 1802, in Hunt 1992, p. 132). This principle was first introduced in Young's study of light and, within some specific contexts (for example, scattering of sound by sound), is still a researched area in the study of sound.
Mathematical description of one-dimensional waves
Wave equation
- in the x direction in space. E.g., let the positive x direction be to the right, and the negative x direction be to the left.
- with constant amplitude u
- with constant velocity v, where v is
- independent of wavelength (no dispersion)
- independent of amplitude (linear media, not nonlinear).[2]
- with constant waveform, or shape
 (waveform F traveling to the right)
(waveform F traveling to the right) (waveform G traveling to the left)
(waveform G traveling to the left)
Wave forms
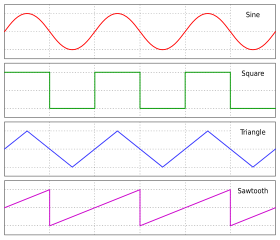
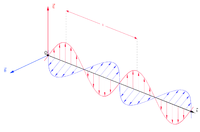
In the case of a periodic function F with period λ, that is, F(x + λ − vt) = F(x − vt), the periodicity of F in space means that a snapshot of the wave at a given time t finds the wave varying periodically in space with period λ (the wavelength of the wave). In a similar fashion, this periodicity of F implies a periodicity in time as well: F(x − v(t + T)) = F(x − vt) provided vT = λ, so an observation of the wave at a fixed location x finds the wave undulating periodically in time with period T = λ/v.[6]
Amplitude and modulation
 is the amplitude envelope of the wave, k is the wavenumber and φ is the phase. If the group velocity vg (see below) is wavelength-independent, this equation can be simplified as:[10]
is the amplitude envelope of the wave, k is the wavenumber and φ is the phase. If the group velocity vg (see below) is wavelength-independent, this equation can be simplified as:[10]Phase velocity and group velocity
The most basic wave (a form of plane wave) may be expressed in the form:
 , makes clear that this expression describes a vibration of wavelength
, makes clear that this expression describes a vibration of wavelength 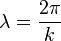 traveling in the x-direction with a constant phase velocity
traveling in the x-direction with a constant phase velocity  .[12]
.[12]The other type of wave to be considered is one with localized structure described by an envelope, which may be expressed mathematically as, for example:
The exponential function inside the integral for ψ oscillates rapidly with its argument, say φ(k1), and where it varies rapidly, the exponentials cancel each other out, interfere destructively, contributing little to ψ.[12] However, an exception occurs at the location where the argument φ of the exponential varies slowly. (This observation is the basis for the method of stationary phase for evaluation of such integrals.[14]) The condition for φ to vary slowly is that its rate of change with k1 be small; this rate of variation is:[12]
Sinusoidal waves
- A is the maximum amplitude of the wave, maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave.
- x is the space coordinate
- t is the time coordinate
- k is the wavenumber
- ω is the angular frequency
- φ is the phase.
The wavelength λ is the distance between two sequential crests or troughs (or other equivalent points), generally is measured in meters. A wavenumber k, the spatial frequency of the wave in radians per unit distance (typically per meter), can be associated with the wavelength by the relation
The angular frequency ω represents the frequency in radians per second. It is related to the frequency or period by
Wavelength can be a useful concept even if the wave is not periodic in space. For example, in an ocean wave approaching shore, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.[17]
Although arbitrary wave shapes will propagate unchanged in lossless linear time-invariant systems, in the presence of dispersion the sine wave is the unique shape that will propagate unchanged but for phase and amplitude, making it easy to analyze.[18] Due to the Kramers–Kronig relations, a linear medium with dispersion also exhibits loss, so the sine wave propagating in a dispersive medium is attenuated in certain frequency ranges that depend upon the medium.[19] The sine function is periodic, so the sine wave or sinusoid has a wavelength in space and a period in time.[20][21]
The sinusoid is defined for all times and distances, whereas in physical situations we usually deal with waves that exist for a limited span in space and duration in time. Fortunately, an arbitrary wave shape can be decomposed into an infinite set of sinusoidal waves by the use of Fourier analysis. As a result, the simple case of a single sinusoidal wave can be applied to more general cases.[22][23] In particular, many media are linear, or nearly so, so the calculation of arbitrary wave behavior can be found by adding up responses to individual sinusoidal waves using the superposition principle to find the solution for a general waveform.[24] When a medium is nonlinear, the response to complex waves cannot be determined from a sine-wave decomposition.
Plane waves
Standing waves

The sum of two counter-propagating waves (of equal amplitude and frequency) creates a standing wave. Standing waves commonly arise when a boundary blocks further propagation of the wave, thus causing wave reflection, and therefore introducing a counter-propagating wave. For example when a violin string is displaced, transverse waves propagate out to where the string is held in place at the bridge and the nut, where the waves are reflected back. At the bridge and nut, the two opposed waves are in antiphase and cancel each other, producing a node. Halfway between two nodes there is an antinode, where the two counter-propagating waves enhance each other maximally. There is no net propagation of energy over time.
-
- A two-dimensional standing wave on a disk; this is the fundamental mode.
- A standing wave on a disk with two nodal lines crossing at the center; this is an overtone.
Physical properties
Waves exhibit common behaviors under a number of standard situations, e.g.,Transmission and media
Waves normally move in in a straight line (i.e. rectilinearly) through a transmission medium. Such media can be classified into one or more of the following categories:- A bounded medium if it is finite in extent, otherwise an unbounded medium
- A linear medium if the amplitudes of different waves at any particular point in the medium can be added
- A uniform medium or homogeneous medium if its physical properties are unchanged at different locations in space
- An anisotropic medium if one or more of its physical properties differ in one or more directions
- An isotropic medium if its physical properties are the same in all directions
Absorption
Reflection
Interference
Refraction
Diffraction
Polarization
Longitudinal waves such as sound waves do not exhibit polarization. For these waves the direction of oscillation is along the direction of travel.
Dispersion
Mechanical waves
Waves on strings
Acoustic waves
Acoustic or sound waves travel at speed given byWater waves
- Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
- Sound—a mechanical wave that propagates through gases, liquids, solids and plasmas;
- Inertial waves, which occur in rotating fluids and are restored by the Coriolis effect;
- Ocean surface waves, which are perturbations that propagate through water.
Seismic waves
Shock waves
Other
- Waves of traffic, that is, propagation of different densities of motor vehicles, and so forth, which can be modeled as kinematic waves[26]
- Metachronal wave refers to the appearance of a traveling wave produced by coordinated sequential actions.
Electromagnetic waves
An electromagnetic wave consists of two waves that are oscillations of the electric and magnetic fields. An electromagnetic wave travels in a direction that is at right angles to the oscillation direction of both fields. In the 19th century, James Clerk Maxwell showed that, in vacuum, the electric and magnetic fields satisfy the wave equation both with speed equal to that of the speed of light. From this emerged the idea that light is an electromagnetic wave. Electromagnetic waves can have different frequencies (and thus wavelengths), giving rise to various types of radiation such as radio waves, microwaves, infrared, visible light, ultraviolet and X-rays.
Quantum mechanical waves

de Broglie waves
A wave representing such a particle traveling in the k-direction is expressed by the wave function:
In representing the wave function of a localized particle, the wave packet is often taken to have a Gaussian shape and is called a Gaussian wave packet.[29] Gaussian wave packets also are used to analyze water waves.[30]
For example, a Gaussian wavefunction ψ might take the form:[31]
The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined by 1/σ. That is, the smaller the extent in space, the larger the extent in k, and hence in λ = 2π/k.

Gravitational waves
WKB method
References
- ^ Lev A. Ostrovsky & Alexander I. Potapov (2002). Modulated waves: theory and application. Johns Hopkins University Press. ISBN 0801873258.
- ^ Michael A. Slawinski (2003). "Wave equations". Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN 0080439306.
- ^ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13–14. ISBN 9780486667454.
- ^ Jalal M. Ihsan Shatah, Michael Struwe (2000). "The linear wave equation". Geometric wave equations. American Mathematical Society Bookstore. pp. 37 ff. ISBN 0821827499.
- ^ Louis Lyons (1998). All you wanted to know about mathematics but were afraid to ask. Cambridge University Press. pp. 128 ff. ISBN 052143601X.
- ^ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN 0470185902.
- ^ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN 3865374190.
- ^ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN 354062001X.
- ^ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. p. 33. ISBN 0521631343.
- ^ a b Chin-Lin Chen (2006). "§13.7.3 Pulse envelope in nondispersive media". Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873.
- ^ Stefano Longhi, Davide Janner (2008). "Localization and Wannier wave packets in photonic crystals". In Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami. Localized Waves. Wiley-Interscience. p. 329. ISBN 0470108851.
- ^ a b c d Albert Messiah (1999). Quantum Mechanics (Reprint of two-volume Wiley 1958 ed.). Courier Dover. pp. 50–52. ISBN 9780486409245.
- ^ See, for example, Eq. 2(a) in Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics: An introduction (2nd ed.). Springer. pp. 60–61. ISBN 3540674586.
- ^ John W. Negele, Henri Orland (1998). Quantum many-particle systems (Reprint in Advanced Book Classics ed.). Westview Press. p. 121. ISBN 0738200522.
- ^ Donald D. Fitts (1999). Principles of quantum mechanics: as applied to chemistry and chemical physics. Cambridge University Press. pp. 15 ff. ISBN 0521658411.
- ^ David C. Cassidy, Gerald James Holton, Floyd James Rutherford (2002). Understanding physics. Birkhäuser. pp. 339 ff. ISBN 0387987568.
- ^ Paul R Pinet (2009). op. cit.. p. 242. ISBN 0763759937.
- ^ Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. p. 208. ISBN 9780780347151.
- ^ See Eq. 5.10 and discussion in A. G. G. M. Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. pp. 119 ff. ISBN 0521826349.; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd ed.). Springer. pp. 261 ff. ISBN 354060443X.; and Eq. 3.5 in F Mainardi (1996). "Transient waves in linear viscoelastic media". In Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy. Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. p. 134. ISBN 9810242719.
- ^ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358.
- ^ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785.
- ^ Seth Stein, Michael E. Wysession (2003). op. cit.. p. 32. ISBN 0865420785.
- ^ Kimball A. Milton, Julian Seymour Schwinger (2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer. p. 16. ISBN 3540293043. "Thus, an arbitrary function f(r, t) can be synthesized by a proper superposition of the functions exp[i (k·r−ωt)]…"
- ^ Raymond A. Serway and John W. Jewett (2005). "§14.1 The Principle of Superposition". Principles of physics (4th ed.). Cengage Learning. p. 433. ISBN 053449143X.
- ^ Newton, Isaac (1704). "Prop VII Theor V". Opticks: Or, A treatise of the Reflections, Refractions, Inflexions and Colours of Light. Also Two treatises of the Species and Magnitude of Curvilinear Figures. 1. London. p. 118. "All the Colours in the Universe which are made by Light... are either the Colours of homogeneal Lights, or compounded of these..."
- ^ M. J. Lighthill; G. B. Whitham (1955). "On kinematic waves. II. A theory of traffic flow on long crowded roads". Proceedings of the Royal Society of London. Series A 229: 281–345. And: P. I. Richards (1956). "Shockwaves on the highway". Operations Research 4: 42–51. doi:10.1287/opre.4.1.42.
- ^ A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN 0486667413. "(p. 61) …the individual waves move more slowly than the packet and therefore pass back through the packet as it advances"
- ^ Ming Chiang Li (1980). "Electron Interference". In L. Marton & Claire Marton. Advances in Electronics and Electron Physics. 53. Academic Press. p. 271. ISBN 0120146533.
- ^ See for example Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2 ed.). Springer. p. 60. ISBN 3540674586. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. p. 57. ISBN 0521620058.,Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. p. 17. ISBN 0521658411..
- ^ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd ed.). World Scientific. p. 47. ISBN 9971507897.
- ^ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2nd ed.). Springer. p. 60. ISBN 3540674586.
- ^ Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3rd ed.). Springer. p. 23. ISBN 0387951415.
- ^ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. p. 677. ISBN 0521598273.















![y=\sin[2\pi(\frac{x}{2\pi}-\frac{t}{2\pi})]](http://upload.wikimedia.org/math/2/1/6/216f44fdac59189c51ecf4d822d93f62.png) progressive sinusoidal wave.
progressive sinusoidal wave.










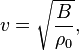



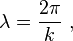




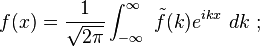
0 comments:
Post a Comment