Quantum chemistry applies quantum theory to the explanation and prediction of chemical behaviour. The majority of quantum chemical investigations, at the time of writing, determine the energies of molecules, using heavy computations based on approximate solutions of the Schrodinger equation. Other quantum chemical studies use semi-empirical and other methods that are also based on quantum mechanical principles, and deal with time dependent problems. Quantum chemical studies relate to the ground state of individual atoms and molecules, to excited states, and to the transition states that occur during chemical reactions. Quantum chemical results include molecular geometry, the strengths and other characteristics of chemical bonds, optical and other spectra, intermolecular forces, chemical reactivity and many other chemical properties and features of chemical behaviour. Many quantum chemical studies assume the nuclei are at rest (Born-Oppenheimer approximation). Many calculations involve iterative methods that include self-consistent field methods. Major goals of quantum chemistry include increasing the accuracy of the results for small molecular systems, and increasing the size of large molecules that can be processed, which is limited by scaling considerations -- the computation time increases as a power of the number of atoms.
Quantum chemistry mathematically describes the fundamental behavior of matter at the molecular scale[1], but can span from elementary particles such as electrons (fermions) and photons (bosons) to the cosmos such as star-formation[2]. It is, in principle, possible to describe all chemical systems using this theory. In practice, only the simplest chemical systems may realistically be investigated in purely quantum mechanical terms, and approximations must be made for most practical purposes (e.g., Hartree-Fock, post Hartree-Fock or Density functional theory, see computational chemistry for more details). Hence a detailed understanding of quantum mechanics is not necessary for most chemistry, as the important implications of the theory (principally the orbital approximation) can be understood and applied in simpler terms.
In quantum mechanics the Hamiltonian, or the physical state, of a particle can be expressed as the sum of two operators, one corresponding to kinetic energy and the other to potential energy. The Hamiltonian in the Schrödinger wave equation used in quantum chemistry does not contain terms for the spin of the electron.
Solutions of the Schrödinger equation for the hydrogen atom gives the form of the wave function for atomic orbitals, and the relative energy of the various orbitals. The orbital approximation can be used to understand the other atoms e.g. helium, lithium and carbon.
An alternative approach
Quantum chemistry is a branch of theoretical chemistry which applies quantum mechanics and quantum field theory to address problems in chemistry. One application of quantum chemistry is the electronic behavior of atoms and molecules relative to their chemical reactivity. Quantum chemistry lies on the border between chemistry and physics. Thus, significant contributions have been made by scientists from both fields. It has a strong and active overlap with the field of atomic physics and molecular physics, as well as physical chemistry.Quantum chemistry mathematically describes the fundamental behavior of matter at the molecular scale[1], but can span from elementary particles such as electrons (fermions) and photons (bosons) to the cosmos such as star-formation[2]. It is, in principle, possible to describe all chemical systems using this theory. In practice, only the simplest chemical systems may realistically be investigated in purely quantum mechanical terms, and approximations must be made for most practical purposes (e.g., Hartree-Fock, post Hartree-Fock or Density functional theory, see computational chemistry for more details). Hence a detailed understanding of quantum mechanics is not necessary for most chemistry, as the important implications of the theory (principally the orbital approximation) can be understood and applied in simpler terms.
In quantum mechanics the Hamiltonian, or the physical state, of a particle can be expressed as the sum of two operators, one corresponding to kinetic energy and the other to potential energy. The Hamiltonian in the Schrödinger wave equation used in quantum chemistry does not contain terms for the spin of the electron.
Solutions of the Schrödinger equation for the hydrogen atom gives the form of the wave function for atomic orbitals, and the relative energy of the various orbitals. The orbital approximation can be used to understand the other atoms e.g. helium, lithium and carbon.
[edit] History
The history of quantum chemistry essentially began with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy radiating atomic system can theoretically be divided into a number of discrete energy elements ε such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula:[edit] Electronic structure
Main article: Computational chemistry#Electronic structure
The first step in solving a quantum chemical problem is usually solving the Schrödinger equation (or Dirac equation in relativistic quantum chemistry) with the electronic molecular Hamiltonian. This is called determining the electronic structure of the molecule. It can be said that the electronic structure of a molecule or crystal implies essentially its chemical properties. An exact solution for the Schrödinger equation can only be obtained for the hydrogen atom. Since all other atomic, or molecular systems, involve the motions of three or more "particles", their Schrödinger equations cannot be solved exactly and so approximate solutions must be sought.[edit] Wave model
The foundation of quantum mechanics and quantum chemistry is the wave model, in which the atom is a small, dense, positively charged nucleus surrounded by electrons. Unlike the earlier Bohr model of the atom, however, the wave model describes electrons as "clouds" moving in orbitals, and their positions are represented by probability distributions rather than discrete points. The strength of this model lies in its predictive power. Specifically, it predicts the pattern of chemically similar elements found in the periodic table. The wave model is so named because electrons exhibit properties (such as interference) traditionally associated with waves. See wave-particle duality.[edit] Valence bond
- Main article: Valence bond theory
[edit] Molecular orbital
- Main article: Molecular orbital theory
[edit] Density functional theory
- Main article: Density functional theory
[edit] Chemical dynamics
A further step can consist of solving the Schrödinger equation with the total molecular Hamiltonian in order to study the motion of molecules. Direct solution of the Schrödinger equation is called quantum molecular dynamics, within the semiclassical approximation semiclassical molecular dynamics, and within the classical mechanics framework molecular dynamics (MD). Statistical approaches, using for example Monte Carlo methods, are also possible.[edit] Adiabatic chemical dynamics
Main article: Adiabatic formalism or Born-Oppenheimer approximation
In adiabatic dynamics, interatomic interactions are represented by single scalar potentials called potential energy surfaces. This is the Born-Oppenheimer approximation introduced by Born and Oppenheimer in 1927. Pioneering applications of this in chemistry were performed by Rice and Ramsperger in 1927 and Kassel in 1928, and generalized into the RRKM theory in 1952 by Marcus who took the transition state theory developed by Eyring in 1935 into account. These methods enable simple estimates of unimolecular reaction rates from a few characteristics of the potential surface.[edit] Non-adiabatic chemical dynamics
- Main article: Vibronic coupling
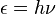
0 comments:
Post a Comment