Capillary action, or capillarity, is the ability of liquid to flow against gravity where liquid spontaneously rises in a narrow space such as a thin tube, or in porous materials such as paper or in some non-porous materials such as liquified carbon fibre. This effect can cause liquids to flow against the force of gravity or the magnetic field induction. It occurs because of inter-molecular attractive forces between the liquid and solid surrounding surfaces; If the diameter of the tube is sufficiently small, then the combination of surface tension (which is caused by cohesion within the liquid) and forces of adhesion between the liquid and container act to lift the liquid
 Capillary action, capillarity, capillary motion, or wicking refers to two phenomena:
Capillary action, capillarity, capillary motion, or wicking refers to two phenomena:
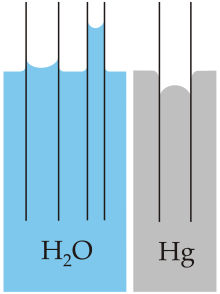
A common apparatus used to demonstrate the first phenomenon is the capillary tube. When the lower end of a vertical glass tube is placed in a liquid such as water, a concave meniscus forms. Adhesion pulls the liquid column up until there is a sufficient mass of liquid for gravitational forces to overcome the intermolecular forces. The contact length (around the edge) between the top of the liquid column and the tube is proportional to the diameter of the tube, while the weight of the liquid column is proportional to the square of the tube's diameter, so a narrow tube will draw a liquid column higher than a wide tube.
In hydrology, capillary action describes the attraction of water molecules to soil particles. Capillary action is responsible for moving groundwater from wet areas of the soil to dry areas. Differences in soil potential (Ψm) drive capillary action in soil.
Capillary action is also essential for the drainage of constantly produced tear fluid from the eye. Two canaliculi of tiny diameter are present in the inner corner of the eyelid, also called the lacrymal ducts; their openings can be seen with the naked eye within the lacrymal sacs when the eyelids are everted.
Wicking is to absorb something and then drain like a wick. Paper towels absorb liquid through capillary action, allowing a fluid to be transferred from a surface to the towel. The small pores of a sponge act as small capillaries, causing it to absorb a comparatively large amount of fluid. Some modern sport and exercise fabrics use capillary action to "wick" sweat away from the skin. These are often referred to as wicking fabrics, after the capillary properties of a candle and lamp wicks.
Capillary action is observed in thin layer chromatography, in which a solvent moves vertically up a plate via capillary action. Dissolved solutes travel with the solvent at various speeds depending on their affinity for the solvent (the mobile phase) or the absorbent coating on the plate (the stationary phase).
With some pairs of materials, such as mercury and glass, the intermolecular forces within the liquid exceed those between the solid and the liquid, so a convex meniscus forms and capillary action works in reverse.
 is the liquid-air surface tension (force/unit length), θ is the contact angle, ρ is the density of liquid (mass/volume), g is local gravitational field strength (force/unit mass), and r is radius of tube (length).
is the liquid-air surface tension (force/unit length), θ is the contact angle, ρ is the density of liquid (mass/volume), g is local gravitational field strength (force/unit mass), and r is radius of tube (length).
For a water-filled glass tube in air at standard laboratory conditions, γ = 0.0728 N/m at 20 °C, θ = 20° (0.35 rad), ρ is 1000 kg/m3, and g = 9.8 m/s2. For these values, the height of the water column is
Sorptivity is a relevant property of building materials, because it affects the amount of rising dampness. Some values for the sorptivity of building materials are in the table below.
.
Etymology
The word "capillary," in the non-medical sense, means narrow tube. The word comes from Latin capillaris ("pertaining to the hair") < capillus ("the hair, prop. of the head") < caput ("head").[2] In medicine and biology, it usually refers to the smallest blood vessels.Phenomena and physics of capillary action

Capillary Flow Experiment to investigate capillary flows and phenomena aboard the International Space Station
A common apparatus used to demonstrate the first phenomenon is the capillary tube. When the lower end of a vertical glass tube is placed in a liquid such as water, a concave meniscus forms. Adhesion pulls the liquid column up until there is a sufficient mass of liquid for gravitational forces to overcome the intermolecular forces. The contact length (around the edge) between the top of the liquid column and the tube is proportional to the diameter of the tube, while the weight of the liquid column is proportional to the square of the tube's diameter, so a narrow tube will draw a liquid column higher than a wide tube.
In hydrology, capillary action describes the attraction of water molecules to soil particles. Capillary action is responsible for moving groundwater from wet areas of the soil to dry areas. Differences in soil potential (Ψm) drive capillary action in soil.
Examples
Wicking is to absorb something and then drain like a wick. Paper towels absorb liquid through capillary action, allowing a fluid to be transferred from a surface to the towel. The small pores of a sponge act as small capillaries, causing it to absorb a comparatively large amount of fluid. Some modern sport and exercise fabrics use capillary action to "wick" sweat away from the skin. These are often referred to as wicking fabrics, after the capillary properties of a candle and lamp wicks.
Capillary action is observed in thin layer chromatography, in which a solvent moves vertically up a plate via capillary action. Dissolved solutes travel with the solvent at various speeds depending on their affinity for the solvent (the mobile phase) or the absorbent coating on the plate (the stationary phase).
With some pairs of materials, such as mercury and glass, the intermolecular forces within the liquid exceed those between the solid and the liquid, so a convex meniscus forms and capillary action works in reverse.
Height of a meniscus
The height h of a liquid column is given by:[3] is the liquid-air surface tension (force/unit length), θ is the contact angle, ρ is the density of liquid (mass/volume), g is local gravitational field strength (force/unit mass), and r is radius of tube (length).
is the liquid-air surface tension (force/unit length), θ is the contact angle, ρ is the density of liquid (mass/volume), g is local gravitational field strength (force/unit mass), and r is radius of tube (length).For a water-filled glass tube in air at standard laboratory conditions, γ = 0.0728 N/m at 20 °C, θ = 20° (0.35 rad), ρ is 1000 kg/m3, and g = 9.8 m/s2. For these values, the height of the water column is
Liquid transport in porous media
When a dry porous medium, such as a brick or a wick, is brought into contact with a liquid, it will start absorbing the liquid at a rate which decreases over time. For a bar of material with cross-sectional area A that is wetted on one end, the cumulative volume V of absorbed liquid after a time t isSorptivity is a relevant property of building materials, because it affects the amount of rising dampness. Some values for the sorptivity of building materials are in the table below.
| Material | Sorptivity (mm min-1/2) | Source |
|---|---|---|
| Aerated concrete | 0.54 | [5] |
| Gypsum plaster | 3.50 | [5] |
| Clay brick | 1.16 | [5] |





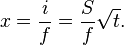
0 comments:
Post a Comment