The enthalpy of fusion, also known as the heat of fusion or specific melting heat, is the change in enthalpy resulting from the addition or removal of heat from 1 mole of a substance to change its state from a solid to a liquid (melting) or the reverse processes of freezing. It is also called the latent heat of fusion, and the temperature at which it occurs is called the melting point.
When thermal energy is withdrawn from a liquid or solid, the temperature falls. When thermal energy is added to a liquid or solid, the temperature rises. However, at the transition point between solid and liquid (the melting point), extra energy is required (the heat of fusion).
In going from liquid to solid (freezing), the molecules of a substance become arranged in a more ordered state. For them to attain the order of a solid, slightly less heat is withdrawn at the point of crystallization. That not withdrawn heat is stored in the form of primarily potential energy to build the solid lattice. In going from solid to liquid (melting), the molecules of a substance become arranged in a less ordered state. To create the relative disorder from the solid crystal to liquid, slightly more heat is added at the point of decrystallization. That energy from heat is utilized to break the solid lattice. This heat does not result in a temperature change, and is called a latent (or hidden) heat.
The heat of fusion can be observed by measuring the temperature of water as it freezes. If a closed container of room temperature water is plunged into a very cold environment (say −20 °C), the temperature will fall steadily until it drops just below the freezing point (0 °C). The temperature then will rebound and hold steady while the water crystallizes. Once the water is completely frozen, its temperature will fall steadily again.
The units of heat of fusion are usually expressed as:

These values are from the CRC Handbook of Chemistry and Physics, 62nd edition. The conversion between cal/g and kJ/kg in the above table uses the thermochemical calorie (calth) = 4.184 joules rather than the International Steam Table calorie (calINT) = 4.1868 joules.
However, to melt ice and raise the resulting water temperature by 20 K requires extra energy. To heat ice from 273.15 K to water at 293.15 K (0 °C to 20 °C) requires:
This equals to a solubility in grams per liter of:

which is a deviation from the real solubility (240 g/L) of 11%. This error can be reduced when an additional heat capacity parameter is taken into account [1]
 the gas constant and
the gas constant and 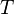 the temperature.
the temperature.
Rearranging gives:
When thermal energy is withdrawn from a liquid or solid, the temperature falls. When thermal energy is added to a liquid or solid, the temperature rises. However, at the transition point between solid and liquid (the melting point), extra energy is required (the heat of fusion).
In going from liquid to solid (freezing), the molecules of a substance become arranged in a more ordered state. For them to attain the order of a solid, slightly less heat is withdrawn at the point of crystallization. That not withdrawn heat is stored in the form of primarily potential energy to build the solid lattice. In going from solid to liquid (melting), the molecules of a substance become arranged in a less ordered state. To create the relative disorder from the solid crystal to liquid, slightly more heat is added at the point of decrystallization. That energy from heat is utilized to break the solid lattice. This heat does not result in a temperature change, and is called a latent (or hidden) heat.
The heat of fusion can be observed by measuring the temperature of water as it freezes. If a closed container of room temperature water is plunged into a very cold environment (say −20 °C), the temperature will fall steadily until it drops just below the freezing point (0 °C). The temperature then will rebound and hold steady while the water crystallizes. Once the water is completely frozen, its temperature will fall steadily again.
The units of heat of fusion are usually expressed as:
- kilojoules per mole (the SI units)
- calories per gram (old metric units now little used, except for a different, larger calorie used in nutritional contexts)
- British thermal units per pound or Btu per pound-mole
Contents[show] |
[edit] Reference values of common substances

Standard enthalpy change of fusion of period two of the periodic table of elements.
Substance | Heat of fusion (cal/g)  | Heat of fusion (kJ/kg)  |
|---|---|---|
| water | 79.72 | 334 |
| methane | 13.96 | 58.41 |
| ethane | 22.73 | 95.10 |
| propane | 19.11 | 79.96 |
| methanol | 23.70 | 99.16 |
| ethanol | 26.05 | 108.99 |
| glycerol | 47.95 | 200.62 |
| formic acid | 66.05 | 276.35 |
| acetic acid | 45.91 | 192.09 |
| acetone | 23.42 | 97.99 |
| benzene | 30.45 | 127.40 |
| myristic acid | 47.49 | 198.70 |
| palmitic acid | 39.18 | 163.93 |
| stearic acid | 47.54 | 198.91 |
| Paraffin wax (C25H52) | 47.8-52.6 | 200–220 |
[edit] Applications
To heat one kilogram (about 1 litre) of water from 283.15 K to 303.15 K (10 °C to 30 °C) requires 83.6 kJ.However, to melt ice and raise the resulting water temperature by 20 K requires extra energy. To heat ice from 273.15 K to water at 293.15 K (0 °C to 20 °C) requires:
- (1) 333.55 J/g (heat of fusion of ice) = 333.55 kJ/kg = 333.55 kJ for 1 kg of ice to melt
- PLUS
- (2) 4.18 J/(g·K) = 4.18 kJ/(kg·K) = 83.6 kJ for 1kg of water to go up 20 K
- = 417.15 kJ
[edit] Solubility prediction
The heat of fusion can also be used to predict solubility for solids in liquids. Provided an ideal solution is obtained the mole fraction (x2) of solute at saturation is a function of the heat of fusion, the melting point of the solid (Tfus) and the temperature (T) of the solution:This equals to a solubility in grams per liter of:

which is a deviation from the real solubility (240 g/L) of 11%. This error can be reduced when an additional heat capacity parameter is taken into account [1]
[edit] Proof
At equilibrium the chemical potentials for the pure solvent and pure solid are identical: the gas constant and
the gas constant and 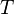 the temperature.
the temperature.Rearranging gives:

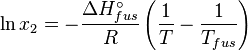






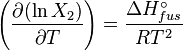


0 comments:
Post a Comment